空気中で空焼き通電されているヒーターからは、2つの形態で、熱が外に伝達されていると考えられます。

(1) 自然対流による放熱
　ヒーターシース付近の空気は、熱せられて密度が小さくなり（軽くなり）、浮力を生じることによって、空気の流れを生じます。この空気の流れで、ヒーターから空気に放熱します。
　放熱量は、ヒーターと空気の温度差に、ほぼ比例すると考えられます。温度差1℃当り、1m²の放熱部（ヒーター）からの放熱量 を h [W/m²・℃] とすると...

　という関係になります。低温で発熱させたヒーターの温度測定結果から、h は10 [W/m²・℃] 前後になりました。

(2) 熱放射による放熱
　ヒーターの熱エネルギーが、電磁波の形で空間を伝わります。高温のヒーターから発生している電磁波は、主に赤外線と可視光線で、温度が上がるほど可視光線の割合が多くなって、明るく見えます。
　放熱量は、絶対温度（K：ケルビン）の4乗に比例しています。　（0℃ = 273.16K）

　ε：放射率は、完全黒体（入射する全てのエネルギーを吸収する）の場合に1で、0の場合は、全てのエネルギーを反射します。一般 に物体はこの中間で灰色体です。

　実際には、ヒーターだけから電磁波が発生しているのではなく、周りの低温の物体からも発生しています。高温の物体（T₁K）から低温の物体（T₀K）への熱伝達を、両者の放射率を同じとして計算すると...

　自然対流／放射の、2つの形態の放熱を考えて、発熱量と表面温度の関係を計算します。

　h = 10 [W/m²・℃] 　T₀ = 293.16 K ( = 20℃) として、ε：放射率が1～0.7のときを計算すると、下のグラフになります。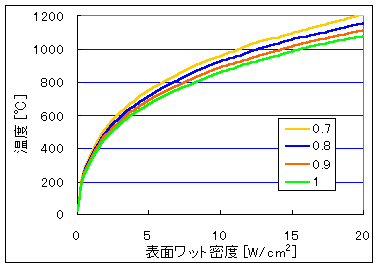

　今回のヒーターでは、限界に近い高温のときは不安定なため不明ですが、900℃以下では、放射率 0.8の線とほぼ同じでした。
　ヒーター表面に黒色酸化皮膜が形成されている、一般の高温空焼用ヒーターの測定では、放射率 0.9 の線に近く、800℃以上の高温では、放射率 1の線に近くなります。自然対流放熱の定数 hは、実際には高温になると少し大きくなっているのかもしれません。

　温度の限界は、ヒーターの表面温度ではなく、シース内部の発熱線の温度によります。カートリッジヒーターに使用されている、ニッケル-クロム系発熱線の溶融温度は、約1400℃です。短時間で断線する高温は、発熱線の温度が1300℃～1400℃の間になっていると思われます。
　また、発熱線を高温で守っているのは、ステンレスが錆びにくいのと同じように、表面に形成された酸化皮膜です。酸素が十分にある大気中では、酸化皮膜が安定していますが、酸素が少ないと不安定になって、発熱線は弱くなります。今回の実験では、耐熱性が高くないSUS304をシースに使用していますので、1000℃付近の高温では酸素を奪い、発熱線の温度限界は低下していたのではないかと思われます。実際、NCF600（ニッケルを70%以上含んだ耐熱合金）をヒーターシースに使用したカートリッジヒーターでは、1100℃以上の高温を確認したことがあります。