LABORATORY熱の実験室
- 熱の実験室
- 熱の実験室-新館
次に3本直列接続について実験してみます。
○実験の方法
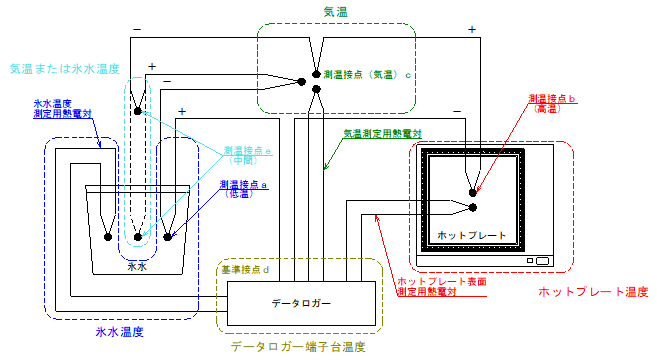
図3. 接続図(熱電対3本直列接続)
なお、中間測温接点eは接続条件により氷水から出し入れを行いました。
以下、表4の接続条件で試験を行います。
表4.接続条件(熱電対3本直列接続)
| 測温接点a(低温) | 測温接点e(中間) | 測温接点c(高温) | 基準接点(気温)c | 基準接点d | |
| (3) | 氷水(0℃) | 気温 | ホットプレート表面(50℃設定) | 気温 | ロガー端子台 |
| (4) | 氷水(0℃) | 氷水(0℃) | ホットプレート表面(50℃設定) | 気温 | ロガー端子台 |
| (5) | 氷水(0℃) | 気温 | ホットプレート表面(100℃設定) | 気温 | ロガー端子台 |
| (6) | 氷水(0℃) | 氷水(0℃) | ホットプレート表面(100℃設定) | 気温 | ロガー端子台 |
○結果
測定温度は表5のようになりました。
表6より、E1とE2、E3の合計であるEとE'は僅かな差はあるものの、傾向として、熱電対の直列接続では回路全体の熱起電力は、各測温接点における熱起電力の合計値となることがわかりました。前述の熱電対2本直列接続の場合と同様になりました。
接続条件(3)について、
基準接点補償分の熱起電力Edは、表5のdの温度より熱起電力換算して求めます。
表5. 測定結果(熱電対3本直列接続)
| 接続条件 | 測定温度[℃] | データロガー 表示温度f [℃] |
熱起電力から 算出した表示温度g [℃] |
f - g 差 [℃] |
||||
| a | b | c | d | e | ||||
| (3) | 0.40 | 26.00 | 50.65 | 26.00 | 30.70 | 27.20 | 27.35 | 0.15 |
| (4) | 0.40 | 0.40 | 50.55 | 26.20 | 30.50 | 0.75 | 0.48 | 0.27 |
| (5) | 0.35 | 25.80 | 98.65 | 30.60 | 30.60 | 76.10 | 76.07 | 0.03 |
| (6) | 0.30 | 0.30 | 98.70 | 30.50 | 30.50 | 50.45 | 50.50 | 0.05 |
| ここで、図3の熱起電力は表6のようになりました。 表6. 測定結果(熱電対2本直列接続―熱起電力)
|
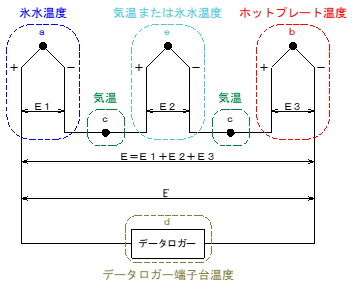 図4. 回路図(熱電対3本直列接続) |
|||||||||||||||||||||||||||||||||||
表6より、E1とE2、E3の合計であるEとE'は僅かな差はあるものの、傾向として、熱電対の直列接続では回路全体の熱起電力は、各測温接点における熱起電力の合計値となることがわかりました。前述の熱電対2本直列接続の場合と同様になりました。
接続条件(3)について、
基準接点補償分の熱起電力Edは、表5のdの温度より熱起電力換算して求めます。
Ed = 1232[µV]
ここで、図4の回路におけるE'とEdの合計(Egとします)を温度換算したものが表5の温度gになります。
Eg = E'+ Ed = 1096[µV]
接続条件(4)、(5)、(6)についても同様に算出しました。○考察
過去の実験では表示温度を熱起電力換算して、換算した熱起電力の合計で表示温度を算出する、という方法をとっていました。今回は、熱電対直列回路全体、および各熱電対の熱起電力を実際に測定し、測定した熱起電力を換算し表示温度としたものと実際の表示温度を比較しました。結果、回路全体の熱起電力と基準接点での熱起電力を合計し算出した表示温度、各熱電対の熱起電力の合計と基準接点での熱起電力を合計し算出した表示温度、並びに熱電対直列回路のデータロガーでの表示温度には、ほとんど差がありませんでした。今回の実験結果より、過去の実験で誤差が出てしまった最大の原因は基準接点温度を気温としてしまったことだと推測できます。実験結果を見ると、気温と基準接点温度であるロガー端子台の温度は約5℃の差がありました。
しかし、実際の表示温度と熱起電力から算出した表示温度には多少の差があり、また差のバラつきがあります。その原因は
また、今回の実験では熱電対を直列に接続し、各測温接点の熱起電力を測定することによって、回路全体の熱起電力は各測温接点における熱起電力の合計値になることがわかりました。各測温接点の熱起電力を電池と見立てれば、電池の直列接続のように見えました。
今回の実験では、熱電対直列回路中の各測温点を合計した熱起電力と全体の熱起電力には差のある結果がありました(表2参照)。これに関してですが、マルチメーターで電圧を測定した際、マルチメーターのワニ口グリップで電線を挟んでいました。この時、マルチメーターの電圧は±50μV程の範囲で変動していましたが、この原因は、しっかりと固定されず、接触抵抗の影響と推測しました。この推測が正しいのかを確かめるため、接続条件(1)と(2)について再試験をしました。再試験では、ワニ口グリップを手で押さえて、しっかり固定した状態で熱起電力を測定しました。また、一つの測定点に対して、ある程度の回数の測定をして、平均値を測定結果としました。測定結果は表7のようになりました。
※ E = E1 + E2 + E0
※ E0は図2のc点(気温)の熱起電力です(今回は0Vとみなせない程の値となったため表記します)。
結果を見てみると、熱電対直列回路の各測温点の合計の熱起電力Eと全体の熱起電力E’はほとんど差が出ていません。また、今回の実験では、熱電対直列回路中の電線をワニ口グリップで挟む際、しっかりと手で押さえて固定したので、接触抵抗の影響は入らず、マルチメーターの瞬間的な電圧値は極端に数値が変わることなく、安定していました(±1~2µV程の変動)。
以上のことから、熱電対を直列接続すると、ホットプレートの温度からロガーの基準温度を引いた値を表示することが分かりました。また、実際に熱起電力を測定したことにより正確なデータを取ることができました。
しかし、実際の表示温度と熱起電力から算出した表示温度には多少の差があり、また差のバラつきがあります。その原因は
- データロガーの基準接点補償回路の精度
補償回路ではロガー端子台の温度を測温抵抗体や半導体を利用して割り出し、そこから得られた温度から疑似的に熱起電力の近似値を出しています。これに関して、端子台の温度を測定するツールの精度、熱起電力を算出する精度が誤差要因になります。 - 熱電対の精度、種類の違い。
- 測定値は同タイミングのものではないこと。
- 測定箇所による温度のバラつき
- 同じ温度差であっても測定温度が異なると熱起電力も異なること。
(例として、0℃-100℃と500℃-600℃の温度差は同じ100℃でも熱起電力が異なること)
また、今回の実験では熱電対を直列に接続し、各測温接点の熱起電力を測定することによって、回路全体の熱起電力は各測温接点における熱起電力の合計値になることがわかりました。各測温接点の熱起電力を電池と見立てれば、電池の直列接続のように見えました。
今回の実験では、熱電対直列回路中の各測温点を合計した熱起電力と全体の熱起電力には差のある結果がありました(表2参照)。これに関してですが、マルチメーターで電圧を測定した際、マルチメーターのワニ口グリップで電線を挟んでいました。この時、マルチメーターの電圧は±50μV程の範囲で変動していましたが、この原因は、しっかりと固定されず、接触抵抗の影響と推測しました。この推測が正しいのかを確かめるため、接続条件(1)と(2)について再試験をしました。再試験では、ワニ口グリップを手で押さえて、しっかり固定した状態で熱起電力を測定しました。また、一つの測定点に対して、ある程度の回数の測定をして、平均値を測定結果としました。測定結果は表7のようになりました。
表7. 測定結果:再試験(熱電対2本直列接続―熱起電力)
| 接続条件 | 熱起電力[μV] | |||||
| E1 | E0 | E2 | E | E' | E' - E | |
| (1) | -1128 | -60 | 871 | -317 | -311 | 6 |
| (2) | -1150 | -96 | 2837 | 1591 | 1611 | 20 |
※ E0は図2のc点(気温)の熱起電力です(今回は0Vとみなせない程の値となったため表記します)。
結果を見てみると、熱電対直列回路の各測温点の合計の熱起電力Eと全体の熱起電力E’はほとんど差が出ていません。また、今回の実験では、熱電対直列回路中の電線をワニ口グリップで挟む際、しっかりと手で押さえて固定したので、接触抵抗の影響は入らず、マルチメーターの瞬間的な電圧値は極端に数値が変わることなく、安定していました(±1~2µV程の変動)。
以上のことから、熱電対を直列接続すると、ホットプレートの温度からロガーの基準温度を引いた値を表示することが分かりました。また、実際に熱起電力を測定したことにより正確なデータを取ることができました。
○まとめ
- 熱電対を直列に接続すると、熱電対直列回路全体の起電力は、各熱電対単体の起電力の合計となる。
- 熱電対の直列回路において、回路全体のデータロガーでの表示温度は、基準温度の温度差の合計で算出した温度よりも、熱起電力の合計から換算した温度のほうがより近くなり、かつデータロガーの表示温度とほぼ同じになる。
- 一般的に、気温(周囲温度)とデータロガーにける基準接点の温度には差がある。また、基準接点の温度誤差がデータロガーの表示温度に大きく影響する。
- 1
- 2
