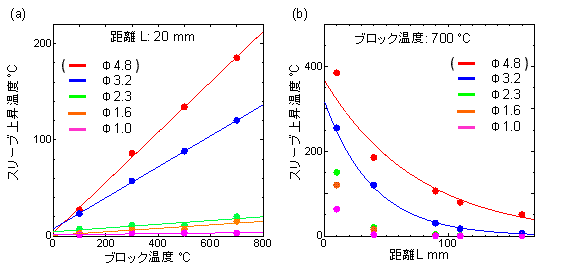
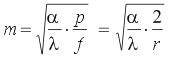今回測定した条件以外でのスリーブ温度を見積もるためにスリーブ温度と加熱ブロック、シース径、距離Lの関係について考察する。
細い棒が熱浴に接している状況を考える。輻射は存在しないものとし、温度は環境温度を基準として測ったものとする。棒の温度は以下の式であらわされる。 |
| T = T0 e-mx |
(3.1) |
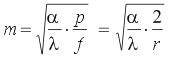 |
(3.2) |
|
| T : 棒の温度 |
T0 : 熱浴の温度 |
x : 熱浴からの距離 |
f : 棒の断面積 |
| p : 断面積の周長 |
r : 棒の半径 |
λ: 棒の熱伝導率 |
α: 棒の熱伝達率 |
|
棒の温度は熱浴の温度に比例し、距離のexp関数として表わされる。また、棒の半径が小さいほど関数の傾きの絶対値は大きくなる。これらは加熱ブロックの温度に比例してスリーブ温度が高くなり、スリーブまでの距離が大きくなるまたはシース径が小さくなるほど急激にスリーブ温度が低くなることを意味している。熱解析結果ではスリーブ上昇温度はブロック温度に比例し、式3.1と対応するが、実験結果では加熱ブロックの温度が低い時、スリーブ温度はブロック温度に比例しなかった。これは、ブロック温度が低い時には環境温度の変化や取付金具からの放熱の寄与の割合が無視できないぐらい大きくなったためだと考えられる。また、輻射による熱の伝達の寄与も考えられる。
図5に図3の一部の拡大図を示した。図5と以上の考察よりスリーブの使用温度限界以下( 90 ℃)となるスリーブまでの距離を見積もることができる。例えば、シース径φ3.2で測定物の温度が600
℃の場合、スリーブ上昇温度はブロック温度に比例するので、図5(a)から700 ℃と500 ℃の間の値を読み取ればよい。よって、室温が20 ℃のとき、スリーブまでの距離を20
mm以上にすればよい。 |
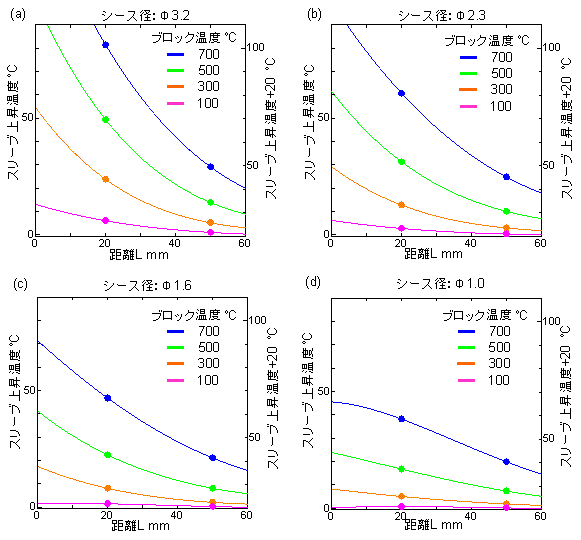 |
| 図5 スリーブまでの距離とスリーブ温度の関係。シース径φ1.0(a)。シース径φ1.6(b)。シース径φ2.3(c)。シース径φ3.2(d)。 |