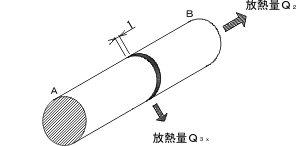
次に、金属棒表面からの放熱量を求めます。金属表面からの放熱量Ｑ_２、Ｑ_３は以下の式により求めます。なお、側面からの放熱は、下図のように金属棒を1mmずつ区切って、その各部分での放熱量の合計で計算します。

　(2)式により得られた各材料の各温度での放熱量（Ｑ_２＋Ｑ_３）を以下に示します。

表. 放熱量計算結果 熱板温度（℃） 放熱量（W） ステンレス 鉄 真鍮 アルミ 100 1.11 1.35 1.38 1.03 150 1.92 2.36 2.46 1.75 200 2.88 3.59 3.76 2.56

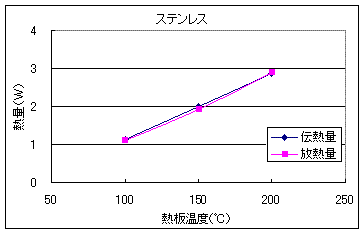
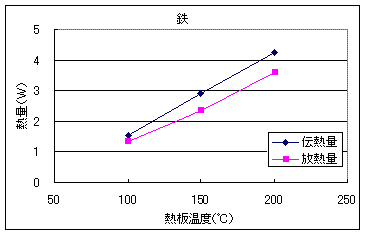
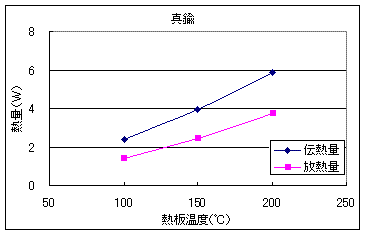
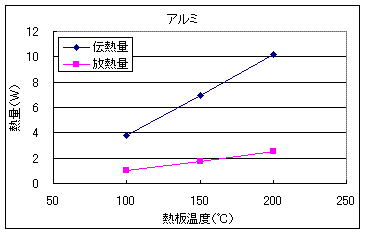
　以上の結果を、伝熱量と放熱量で比較してみます。以下に比較した図を示します。

　以上の結果より、ステンレスは伝熱量と放熱量がほぼ同じ数値となりました。しかし、鉄、真鍮、アルミについては放熱量が少なくなっており、特にアルミについてはかなりの差が出てしまいました。

　今回の実験では、ステンレスのように熱伝導率の低い金属では、断熱をしなくても、伝熱量と放熱量はほぼ同じ値となり、熱エネルギーは保存されていましたが、真鍮やアルミのように熱伝導率が高い金属では、伝熱量と放熱量に大きな差が出てしまいました。これは、熱伝導率の高い金属は放熱量も多く、Ｂ面に熱が伝わるまでに多くの熱を失っているために、Ａ面とＢ面の温度差が大きくなってしまったために、伝熱量が多くなってしまったためと考えられます。
　今後、(1)の金属棒側面を完全に断熱した場合の実験を行い、どの金属でも伝熱量と放熱量が等しくなることを確かめたいと思います。